![[Fig. 5]](../plaatjes/proefschrift_fig_05.gif)
Fig. 5
Jos Kunst home page: Nederlands | English
by Jos Kunst (1978)
| << 3: Some mathematical aspects | Contents | 5: Chopin op. 28 nr. 7 >> |
We will now, availing ourselves of the groundwork laid down in chapter 1, turn again to the main subject of chapter 0's later stages (cf 0.5 – 0.7): the unlearning-plus-learning (UNLL) process. We shall start out from a concrete example that is so simple and unspecific musically that not only no reader will have any trouble following it, but also we may presume it to provide a convenient paradigm case representing an important class of UNLL processes.
Suppose you are in a concert audience, listening to a music new to you (cf the M-type case of 1.2.3); suppose further that all tones actually produced are well below middle c. Suppose that this is, for the moment, all you have in the way of this music's law-likeness: there are only low tones.
Suddenly you hear a tone more than an octave above middle c. The musical law you were relying upon is broken: if you prove incapable of finding (or constructing) any new one that fits the music, you will lose your grip on it: cease to understand it. (Needless to say, things of this type do actually happen. Moreover, they are even likely to be possible parts of any otherwise successful listening process, provided we relate the "losing one's grip", the "ceasing to understand", to certain specific aspects only, and not to the whole of our orientation in the given music.) Now if we write "p" for "there are only low tones", we might represent this by the following diagram. (Its precise graphical form is not important now; it will be explained later (2.1.3).)
Column 0, as given in Fig 5, reflects the history of the law □p. The first two worlds, w00 and w01, present no problem: their interpretation has been sufficiently dealt with in 1.2.3, and they are just a version of Fig 4 pruned of some redundancies. New, however, are w02A, which has no modalized statements at all,and which, in view of its label, seems a sort of annex to w02; and w02 itself, which contains a formula of a new type.
Clearly, w02A(1) (formula (1) in w02A) means: "it is not the case that there are only low tones", or, alternatively, "there is (at least) one not-low tone"; in w02 this leads to a modalized statement (w02(1)) which says that the law □p has been broken: two things are asserted of it, first: it does not obtain (¬□p, because of w02A); and second: at some time it did obtain (◊□p, by reference to w01); these two things are jointly asserted: ¬□p∧◊□p.
Formulas of this form are going to play a crucial role in our diagrams: they will occur in all worlds which digest changes in law-structure. Formally they are nothing more and nothing less than the negation of ◊□p → □p, which is the usual axiom of S9 (S5!):
¬(◊□p → □p) ↔ ◊□p∧¬□p ↔ ¬□p∧◊□p
and that may be taken to mean that precisely in as far as any listener had the feeling that he knew the future as well as the past (which would imply a symmetrical R-relation!) he will feel that "the impossible has happened", that contradictions come true, and logic is no longer bivalent: truth values collapse into meaninglessness. In short, he will lose his grip on the world. The case of the listener who had no such strong presumptions on the future is less tragic, but still serious: at Fig 5's w02 (as in all cases analogous to it) no law is asserted, and no non-trivial law is assertable.
Now back to our concert audience of 2.0.1. Suppose that there is also a listener who tackles the same aspects of the music with a conceptual apparatus somewhat richer than yours. Suppose he has had some musical training and knows the instruments. For him, "all players use their instruments' lowest register only": call this "q". At the same time he is aware that the music keeps avoiding the high instruments in the ensemble, so that also the ensemble's low register only is activated. This listener will thus have, by way of musical law, □(p∧q)
Suddenly, enters the piccolo, playing d'', the instrument's lowest tone, but definitely not low in the ensemble's overall register, in fact more than an octave above middle c. Clearly, now, for our second listener, the law □(p∧q) is broken, but he still has □q.
Finally, to end this chain of expository and heuristic suppositions, suppose that our two listeners are really one and the same person, in the sense that the second is a potential version of the first, one that he becomes aware of when his somewhat lazy conceptualization of the music gets him into trouble: a listener that he might as well, or better, have been. In that way he becomes aware of a possible past that is richer, and that will help him out of the present trouble by permitting him to continue understanding the music. He thus brings about a reappraisal of past and present; new insight is gained, and a continued grip on the music is assured.
Let the following diagram represent the frame in which this process is possible.
w12A is here seen to serve as a sort of pivot point: through it (the relation R is transitive!) a new "possible past", specified by w10 and w11, becomes accessible, and the situation now gives rise to two possible results: one (w02) a dead end, in which no law is assertable, and the other (w12) one in which a musical law survives. It is thus a cross-roads, a switching-point, permitting one to change over from one column (track) to another.
Cognitively, or psychologically, this will mean that a certain set of perceived features of the music may give rise to two asymmetrically related different constructions in the sphere of musical law-likeness (cf also 2.5.1).
The concert audience story told in the foregoing section (2.0) is meant to stand for a class of such cases, and, accordingly, we will want to consider the letters p and q of Fig 6 not as constants, but as propositional variables. Fig 6 then becomes a general frame from which particular cases are obtained by substitution, as detailed below.
We will proceed as follows. With in principle arbitrary [1] ordered pairs of propositions <p,q> reflecting musical behaviour we will associate a specific frame-for-a-process, viz. the one given in Fig 6. Any definite rule governing such an association is, in mathematical language, called a function. The one we are now describing we will call the two-place Bivalence Function (this beautiful name is explained elsewhere: cf 2.5.1, but also 2.0.1); it takes ordered pairs of propositions as its arguments, and associates with them the structures that result from substituting the first of each pair for p, and the second for q, in the diagram given in Fig 6. These resulting structures, the values of the function, will be referred to as BivF( , ) ("BivF" pronounceable as "biff"), with the two substituted propositions filling the two open places. Thus the expression "BivF(a,b)" will name the structure resulting from writing a wherever p occurs, and b wherever q occurs, in Fig 6's diagram.
The foregoing obviously aims at no such thing as full mathematical rigour, which would certainly turn out to be too cumbersome for our purpose. But it may serve; no possible ambiguities, we take it, are likely to become at all dangerous. It will be best to proceed by practical examples; thus, e.g., in the case of substitution instances of Fig 6's schema. In principle, they are easy to produce by the reader. One specific problem is likely to crop up: that of logical calculation. Notably, in the twoplace Bivalence Function, two formulas (parts of formulas) may admit of reduction to a simpler form: p∧q, occuring in w10, w11 and w12, and ¬p∧q, occuring in w12A. (For instance: in BivF(a,a∨b): a∧(a∨b) is reducible to a and ¬a∧(a∨b) to ¬a∧b ) Therefore only the most elementary computational problems may be expected to arise; the reader is referred to, e.g., the first twenty pages of Hughes & Cresswell 1968. We give here only the full list of symbols that, apart from proposition letters, may occur in formulas.
| Sign | Reading | |
|---|---|---|
| Necessity sign for musical laws | □ | Necessarily; always (with respect to past and present – cf. 1.1.1) |
| Possibility sign for musical laws | ◊ | Possibly; at some time (in past or present – cf. 1.1.1) |
| Negation | ¬ | Not ... |
| Conjunction | ∧ | Both ... and ... |
| Disjunction | ∨ | Either ... or ... or both |
| Implication | → | If ... then ... A→B =def-A∨B |
| Strict implication | ⇒ | Always, if ... then ... A⇒B =def □(A→B) |
| Equivalence | ↔ | ... if and only if ... A↔B =def (A→B)∧(B→A) |
| Strict equivalence | ⇔ | Always, ... if and only if ... A⇔B =def (A↔B)∧(B↔A) |
| Brackets | ( ) | |
Two substitution instances of Fig 6 giving rise to interesting more or less 'degenerate' borderline cases are given here. The first is BivF(p,T):
where T stands for any PC tautology, e.g. p→p. A tautology is a proposition which, on logical grounds alone, could not possibly be false in any world. Therefore, asserting T is wholly uninformative, asserting p∧T amounts to asserting just p, and asserting ¬p∧T to just ¬p. □T, where T is a PC tautology, is an S7/S8 tautology. It is readily seen that there is really nothing to choose between columns 0 and 1: to all intents and purposes they are the same column. Therefore we will let the right-column worlds collapse into the corresponding left-column ones, and what is left is precisely Fig 5, our case of a listener 'dropping out' of the music.
Such collapsing of columns need not always be total: it may happen that only the two "possible pasts" collapse (i.e. w10 into w00 and w11 into w01) and that w12 remains distinct from w02. As a case in point we mention BivF(p,q→p):
which represents, in one plausible interpretation, the limiting of the area of application of a law: first one thought that it obtained unconditionally; then, having digested some disturbing information, and changed columns succesfully, one finds that it only applies to the case in which q is true.
In the two-place Bivalence Function is embodied an assumption that, at least in our opinion, might well prove unwarrantable for many interesting cases. In any newly discovered possible past at least the laws that characterized one's original past hold: all right columns are at least as strong as the left ones. We now describe a function which is free from that assumption, but in which the ensuing weakening of the link between the columns is not such as to make it wholly uninteresting.
In a manner analogous to 2.1.1 we now define a function, henceforth called the three-place Bivalence Function, which associates with ordered triples <p,q,r> of propositions, each reflecting musical behaviour, the frame-for-a-process given in Fig 9. Arguments of the function will thus be ordered triples of propositions; the values of the function are the structures resulting from substituting in Fig 9 the first of each triple for p, the second for q, and the third for r. Any such resulting structure will be referred to as BivF( , , ), with the three substituted propositions filling the three open places.
In w10, as in w11, (1) is implied by (2), and therefore one might propose that we drop (1) in both cases. We will argue against it, for the following two reasons. First, (1) represents a part of the new 'possible past' that is meant to survive, and the corresponding formula in w12 is not redundant: in fact it guarantees that w12A(1): ¬p will not be forgotten there. Now because of the fact that the right column's first two worlds, in their role of newly discovered possible past, are taken to be constructed because of the failure of □p as a law, any law that still holds and that makes reference to p will be entitled to some extra weight. Second, the formula p→(q∧r) could be taken to be what is immediately available of the "only if" part of a definition of p in terms of q and r (or, alternatively, of the "if" part of a definition of q∧r in terms of p). Apart from w12A it thus constitutes an important link between the two columns, a retrospective link, well worth emphasizing, especially because in the three-place Bivalence Function the two columns are, in fact, much more loosely joined together than in the two-place case.
As we did in the two-place case, we will give now two instructive 'degenerate' substitution instances of the three-place BivF.
First, the two-place Bivalence Function can be considered as a limiting case of the three-place one: BivF(p,p,q) is easily seen to be reducible to BivF(p,q). The formula we dealt with in 2.2.2 becomes redundant wherever it occurs, and has none of the functions we mentioned there; consequently, it may be dropped. The reader is advised to verify this.
We will then also have that BivF(p,p,T) reduces to Fig 5.
Second, we mention a limiting case arising only with the threeplace Bivalence Function: BivF(p,q→p,T), which takes the following form. (PC formulas reducing to tautologies are represented by just T.)
Here the two "possible pasts" are clearly different, and so are w02 and w12. But in an important sense there is really nothing to choose between these last two: neither can assert any surviving law. An interesting and perhaps plausible reading of it could be that it represents a failing strategy. One has constructed a new past, but the same event that destroyed the original law □p also proves fatal to the new law q⇒p. lt would seem plausible, then, to suppose the possibility of a second try; and that could be represented by extending the Fig 10 frame, e.g., by concatenating the two BivFs BivF(p,q→p,T) and BivF (q→p,r→(q→p)) (The reader is asked to verify that, because of the fact that tautologies may be deleted throughout, the first two columns of Fig 11 are indeed identical to Fig 10; furthermore, that the new BivF, whose left column is identical to the right one of the first, is really a substitution instance of Fig 8: therefore no new past need be constructed).
Columns are numbered according to Rule B (cf 1.2.3).
It is perhaps worth noting that a listener could have reached the sarne end-point, starting from the same beginning-point, by the shorter route of BivF(p,q→p,r→(q→p)). Verification that this amounts precisely to
is left to the reader.
In Bartók's 5th string quartet, 2nd movement, the bars 11–21 of the 1st violin part are the following.
There are surely a number of different ways of understanding this music, as it is given, within its proper context. The problem of the completeness of our descriptions, however, will have to wait until the next chapter. For now, we will only try to present one defensible way of understanding the above notes. It exploits the following concepts. At A the note b2 has imposed itself as a sort of "ceiling"-note: the music has worked its way upwards, and in spite of an increase in dynamics (p) it does not succeed in getting past it. (Some would perhaps say that it gives up already.) Then, at B, after a longer pause, and getting under way again in a quasi-hesitating manner, it starts effortlessly (più p) on c3. One might say that by no longer treating the b2 as an obstacle, it is, as if by miracle, lifted: the "ceiling" simply is no longer there. Thus, point may serve as an "ear-opener", in the way given in Fig 13. First one remarks the sudden absence of the "ceiling"; then one sees (or, if you prefer, "feels") that this ceiling-function is bound up not only with not getting past a certain note, but also with the linking up of higher pitch with higher dynamics, more effort, as vocal and instrumental practice have prepared us to accept it. The whole process separates in our minds pitch from effort (dynamics), and thus, as it were, creates a parameter: before, these two were one and the same [2].
The rhythm, and the other three parts, and their rhythm, do much to help this UNLL process.
BivF(a,b→c,d↔(b∧¬c))
Non-logical constants:
a = b2 is a "ceiling"
b = the music climbs
c = the music expends energy (cresc)
d = the music goes higher than b2
Fig 13
The first 10 bars of Debussy's piano prelude "La sérénade interrompue" are given in Fig 14. The piano "plays" (in the sense of role-playing) a guitar-like instrument, which in its turn "plays" a melody-instrument using only small intervalls. Consequence of this is that it has to "go through its registers" (before A) in order to achieve some ambitus. Then (at A), suddenly, the same ambitus is produced, in the same articulation-form, by the "guitar"'s switching over to a different "instrument", capable of chordal playing of a sort, and the whole ambitus F–f is now filled at once, with no mobility through registers involved. The dynamics underline this break: sudden mf.
BivF(a,b→c,b↔d)
a = the music behaves like a melody-instrument using only very small intervals
b = ambitus is produced
c = there is vertical mobility, as if changing registers
d = the octave F–f is spanned, using the characteristic ![]() articulation (. . .)
articulation (. . .)
Fig 15
What is "learned" here, is the possibility of two ways of going about the same thing: the many resemblances between the musics before and after A suggest very specific ways of comparing them. Ambitus is loosened from melodic behaviour.
(Remark. The informativity (in the sense of "newness") of UNLL processes certainly can wear away, and those of us who, e.g., have since long known this guitar-behaviour will only go through the UNLL process of its being transposed to the piano ( a BivF(p,q) form process). But I think that this wearing away is countered in some degree by the listener's dividing himself in two, as it were, one of these being new to the UNLL process. Thus, by "playing stupid", the pleasure of learning may be sought again and again.)
As a last example, one endowed with great historical and theoretical prestige, and better studied, perhaps, than any other musical UNLL process: modulation, here in its most general form, demonstrating its basic isomorphism with the cases treated thus far.
BivF(a,b→a,(b→(c∨a))∧(c→¬a))
Fig 16
where
a = we have tonality (key ) T
b = we have some specifiable succession of notes or chords
c = we have tonality U.
The "specifiable succession of notes or chords" mentioned under b are the 'pivot' notes/chords linking up the two keys in each given modulation.
In order to demonstrate the versatility and possible general usefulness of the Bivalence Function, two examples are given from fields unrelated to music.
Consider the following cartoon.
Fig 17
If we establish the following reference list:
a = the arrow hits the apple
b = the arrow reaches its target
c = the arrow hits the bull's eye
we could make, e.g., the following proposals for formalizing it by BivFs:
A two-place BivF whose columns collapse into one before w12A. It reads the cartoon as follows: first, one thought that the arrow was only meant to hit the apple, as in the William Tell story, after, one finds that it was meant, by a still more singular feat, to hit both apple and bull's eye.
Here the letter c does not appear in the model. The difference from the preceding one is that here it is only assumed that the arrow was meant for the bull's eye (c collapses into b); on its way towards it, it just passed through the apple.
BivF(a→b,a↔b,c→(a∧b))
Fig 18
Finally, to close our set of examples, a treatment of what happens in metaphorical discourse. It has the particularity of combining two BivFs in a sort of tandem: both use the same set of concepts, both assign the same truth-values to all atomic wffs in their respective w12A, and they are each other's substitution instances in the following way:
for a in the first, to get the 2nd, substitute e and vice versa
for b in the first, to get the 2nd, substitute ¬c and vice versa
for c∧e in the first, to get the 2nd, substitute a∧d and vice versa
for d in the first, to get the 2nd, substitute ¬b and vice versa
In order to make ourselves clear, we will quote throughout, as an example, the expression "the Corsican Eagle", for Napoleon, with no excuses offered.
Reference list:
a = we have the signifiant of the comparant ("eagle")
b = we have the signifié of the comparant (/eagle/)
c = we have the signifié of the comparé (/Napoleon/)
d = we have a comparé-determined context ("the Corsican... ")
e = we have some comparison-determined concept(s)
We will then have the BivFs written out in Fig 19.
BivF(a→b,a→¬d,(a∧d)→c∧e))
Fig 19a
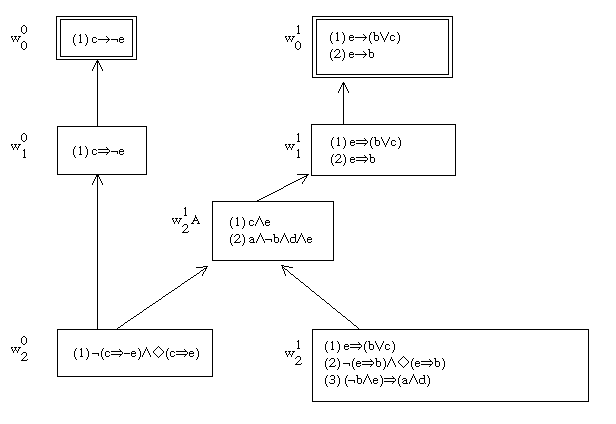
BivF(c→¬e,e→b,(¬b∧e)→a∧d))
Fig 19b
The first of the two does not separate c from e, the second does not separate a from d. The first differentiates between a and d, the second between c and e. The first seems more signifiant-oriented, the second more signifié-oriented.
We will round things off, for the moment, with some remarks concerning meaning and possible use of our Bivalence Function, in as far as any judgment can be formed at the present stage concerning them. We will be taking up again the same subject below (cf 4.2 and 4.3).
What a BivF takes on to represent is the cognitive frame within which a change of value of some semiotic unit may take place. It is heuristically useful to say that, at the crucial moment, this unit is viewed in two perspectives at once, and, accordingly, takes on two, often mutually exclusive, "values" . That is where the Bivalence Function got its name from (cf 2.0.1, toward the end). Although the semiotic unit concerned had one of its values before, and, in principle, only the other after the UNLL process, it cannot be properly understood without taking into account the exact way in which two perspectives, two contexts, for a moment intersected on it.
Bivalence Function may be described as minimal buildingblocks for labyrinths. In as far as every music, poetical text, novel, painting etc. functions as a labyrinth-to-be-got-through, BivFs are the proper tool to represent them formally. In the next chapter we will try to put to the test their power by using a small but, in some sense, complete piano piece as material to be formalized. What gets formalized, the reader will know by now, are not the notes, but the interaction of concepts manipulated in order to understand them.
The chief use of the Bivalence Function will be, it seems to us, that it will provide a starting-point for building up a useful metalanguage ; having formalized some adequate "understandings" of some musics, we will still want to make one further step, without which most of the possible profit of a formalization would be lost: BivFs will have to be classified and catalogued for both the variants of their internal structure and those of the ways they interlock; this will constitute the beginning of the metalanguage, which will enable us to "compare" the understandings mentioned above and to generate in that way hypothesized larger frames defining their possible relationships.
| << 3: Some mathematical aspects | Contents | 5: Chopin op. 28 nr. 7 >> |
Jos Kunst home page Nederlands | Jos Kunst home page English | Sitemap