Jos Kunst home page: Nederlands | English
door Jos Kunst (1973)
Lezing gehouden op 16 mei 1973 in het Studium Generale aan de Technische Hogeschool Eindhoven,
oorspronkelijk verschenen in: Muzikale perspektieven: lezingen gehouden op 2, 9 en 16 mei 1973 in het
Studium Generale aan de T.H. Eindhoven. Eindhoven: Studium Generale, Technische Hogeschool, 1973, p. 15-27.
Vermoedelijk door een redactie ingebrachte spellingsvarianten die Jos Kunst nooit geschreven zou hebben ('konkreet',
etc.) heb ik stilzwijgend aangepast.
Muziek, dames en heren, is voor de meesten van U ongetwijfeld een soort vakantie-onderwerp. Daarmee doel ik op het feit dat voor U muziek, in tegenstelling tot wiskunde, iets is dat het leven versiert, en niet iets "waar je iets mee kunt doen". Professioneel zijn de meesten Uwer er trouwens niet bij betrokken.
Het geeft dan ook te denken, dat wanneer we de bij de muziek wèl professioneel betrokkenen, de musici, naar hun mening vragen, we ook van hen bijna altijd te horen krijgen dat je "met muziek niets doen kan", buiten de vrije keuze (?) dan die men altijd nog heeft van wàt, welk gebeuren, welke situatie, welke mededeling eventueel, men met zijn product zal gaan versieren.
Een verontrustende eenstemmigheid is dit tussen mensen die in de muziek hun leven investeren en mensen die dat niet doen. Want er zijn er toch ook die wel degelijk vinden dat er met muziek iets te doen is, en die, als ik het wel heb niet ver hier vandaan, hebben uitgeprobeerd welke muziek de meest efficiënte begeleiding oplevert voor het werk aan de lopende band. Een muziek dus die de mensen in een soort halfslaap houdt, net wakker genoeg om routinehandelingen te verrichten, net niet wakker genoeg om zich af te vragen wat ze eigenlijk aan het doen zijn. Muziek, voor dit doel gebruikt, blijkt te moeten voldoen aan redelijk precies te omschrijven eisen voor wat betreft tempo, ritmiek, gebruikte toonhoogten, sterktegraden enz.
Een bepaald soort mensen blijkt dus toch van mening, en kan die mening ook proefondervindelijk toetsen, dat je met muziek wel wat doen kan dat meer is dan versieren alleen, namelijk het denken van mensen beïnvloeden.
Hoe deze beïnvloeding precies in zijn werk gaat is een semiologisch-theoretische kwestie; deze hier en nu aan te pakken zou zeker te veel tijd kosten en ons ook voeren op terreinen die buiten het bestek van deze voordracht vallen.
We beperken daarom ons uitgangspunt tot enkele zeer elementaire constateringen. In het algemeen zal niemand verbaasd zijn mensen te horen getuigen dat "muziek hen wat doet". Dan blijken specifieke ervaringsprocessen gebonden te zijn aan specifieke stukken, of specifieke muzieksoorten. Muziek, zou men kunnen zeggen, overkomt de luisteraar als een soort situatieverloop, dat hij meemaakt: bepaalde verwachtingspatronen worden gewekt, er wordt op een al of niet subtiele manier al of niet van afgeweken, er is iets als een engagement.
De centrale vraag die wij ons hier stellen is de volgende: kunnen wij deze ervarings- en denkprocessen formaliseren op een wijze die wetenschappelijk zin heeft, d.w.z. zodanig dat controleerbaarheid, en eventueel misschien zelfs toetsbaarheid in een experimentsituatie, gegarandeerd zijn? Ik voorzie hierbij onmiddellijk al drie objecties.
De eerste houdt in dat muziek een "te persoonlijke zaak" is, en als zodanig hopeloos subjectief. (Iets anders dan de fysieke gebaren van de musici blijken de componisten dan niet gestuurd te hebben. Des te erger voor hen.) Er valt een antwoord op te geven waarvan misschien aangenomen mag worden dat het het overgrote deel van de subjectieve variabiliteit voor ons grijpbaar kan maken, formaliseerbaar als het gegeven stuk zelf dat is. Het is gebaseerd op de idee de verschillende persoonlijke verledens die de verschillende reacties bepalen te duiden als verschillende muzikale verledens. De verschillen tussen de luisteraars, welke die ook zijn, zullen in ieder geval ook de verschillen omvatten tussen de muzikale ervaringen uit het verleden, en misschien ontstaan dáár wel de meest directe en beslissende "persoonlijke" reacties. Als onze formalisatie-aanpak ons in staat zou stellen hier een greep op te krijgen zou in elk geval van een substantieel deel van de subjectieve variabiliteit rekenschap gegeven kunnen worden: die zou dan neerkomen op een spel van relaties van een gegeven muziek met andere muzieken: een zaak van muzieken-onder-elkaar.
De tweede objectie stelt dat muziek een zaak is van "gevoel", en daarom niet grijpbaar voor enig rationeel taalsysteem. In dit verband is het zinnig na te gaan hoe het in het algemeen gesteld is met de grijpbaarheid van gevoelens: hoe heeft men ze in het verleden aangepakt? In gefossiliseerde vorm zijn er een aantal terug te vinden in de traditionele italiaanse tempo-aanduidingen voor muziek. Ook in commentaren over muziek duiken vaak termen op die voor gevoelens staan, en die in fossiliseringsgraad nauwelijks onderdoen voor de genoemde tempo-aanduidingen. Werkelijk genuanceerder en bovendien een wijder veld bestrijkend (en daarmee wezenlijk bepalend voor ons bewustzijn!) is natuurlijk de aanpak die in de verbale kunsten te vinden is, in de psychologische roman vanaf de 17e eeuw, in de lyrische poëzie. En als we nagaan hoe daar gevoelens worden beschreven, dan zien we dat dat, behalve door het zeer beperkt fonds van woorden die ze rechtstreeks aanduiden, eigenlijk uitsluitend gebeurt via beschrijvingen van situaties. Zowel subtiele nuanceringen als op het moment van schrijven nieuwe gevoelens worden in woorden weergegeven (gemaakt) door de beschrijving van de situatie die ze bepaalt. Nieuwe gevoelens zijn dus nieuwe situaties. Als ons formalisatiesysteem daarom in staat zou zijn de situaties vast te leggen waarin een muziek de hoorder brengt, dan zou ze daarmee meteen al een greep hebben op de wijze waarop "gevoelens" door haar worden gestuurd. [1]
De derde objectie die ter tafel zou kunnen worden gebracht en die hier genoemd zal worden is gebaseerd op een aprioristische angst voor wetenschap en vooral wiskunde die men bij velen en in het bijzonder bij musici aan kan treffen. De vraag die men dan stelt luidt: Is een mathematische methodiek niet per definitie te weinig soepel om adequaat te kunnen reageren op wat er in iets als muziek allemaal aan de orde komt? Wij zullen op deze vraag geen vierkant antwoord kunnen geven, maar zullen dus ook de erin vervatte suggestie van de onbruikbaarheid van een mathematische aanpak niet a priori tot de onze maken. We moeten het maar zo serieus mogelijk proberen, want aan een eventueel geheel of gedeeltelijk slagen van deze onderneming zijn enorme voordelen verbonden: met name het eindelijk (geheel of gedeeltelijk) realiseren van controleerbaarheid, toetsbaarheid, objectiviteit bij het beschrijven van wat muziek eigenlijk doet, en daarmee een kans op het halen van de muziek uit het maatschappelijk verdomhoekje waar ze nu zit, en van waaruit ze alles maar moet "versieren".
Xenakis, en dat moeten wij in hem waarderen, heeft dit soort ideeën als eerste aan de orde gesteld, zij het dan in termen die enigszins te denken geven. Hij heeft het over een herintegratie van abstract-wetenschappelijk en concreet-artistiek denken, en schijnt er zodoende van uit te gaan dat in enige mythische oertijd (b.v. de Griekse) er een eenheid bestond waarin wetenschappelijk en ander denken samenvielen. We doen er beter aan deze mythe (juist omdat het er een is) voorlopig maar te vergeten, en onze aandacht te richten op de methoden die Xenakis bij zijn streven tot integratie aanwendt. Dan blijkt jammergenoeg dat hij, behalve kritiekloos in te haken op traditionele mythen, ook nog werkt aan zijn persoonlijke mythe, zijn "image", zoals dat in reclametermen heet. In enkele werken van hem vinden we boven en tussen de noten boole-algebraïsche formules staan, die zonder precisering van de betekenis der gebruikte variabelen niet te controleren zijn, en dus enkel en alleen op de lezer de boodschap overbrengen dat het hier om een erg geleerde, ja mathematische muziek gaat, waarvan het productieproces heel anders geweest is dan dat van gewone muzieken. Proberen we dan toch na te gaan wat er zoal staat dan ontdekken we dat het in geen geval adequaat zou kunnen zijn als weergave van muzikale denkprocessen. Het zijn uiterst elementaire formules, uitsluitend handelend over toonhoogten(!) en bevattend intersecties en verenigingen (en combinaties daarvan) van een uiterst beperkt aantal variabelen; ze volgen in het stuk eenvoudigweg op elkaar. Het is wel zeker dat deze rekentechniek, in wezen neerkomend op die der elementaire propositie-logica, te simpel is om het denken weer te geven zoals het denkend subject dat meemaakt. Al veel geschikter voor dergelijk werk zou de predikaat-logica zijn: het feit bijvoorbeeld dat de aloude syllogismenleer een onderdeel is van de predikaat-logica wijst daar al op. Verder (en er is een evident verband!) het feit dat de predikaat-logica formeel ten nauwste verband houdt met de natuurlijke talen: de in alle leerboeken, en niet alleen die voor beginners, gebruikelijke "vertalingen" van formules in verbale zinnen, met het doel de "talige" intuïtie van de lezer te mobiliseren, vindt daarin zijn zin, en er blijken, wanneer men deze voorbeelden analyseert, impliciete aannamen te bestaan over de status van argumenten enerzijds en predikaten anderzijds, die ontleend schijnen aan de in enkele (indo-europese) talen gebruikelijke zinsstructuren. Ook de traditionele oppositie concreet-abstract blijkt dan een rol te spelen.[2]
Voor wat een toepassing op muziek betreft, zouden speciaal de genoemde conventies over de status van argumenten en predikaten, met name waar het de "vertaalregels" betreft, onoverkomelijke moeilijkheden opleveren. Immers, willen wij ons houden aan een eerste orde logica, dan mogen we niet kwantificeren over predikaten, en dan moeten we dus goed nadenken over, en kriteria vinden voor, het interpretatieverschil van argumenten en predikaten. Het probleem laat zich omzeilen door te kwantificeren niet over argumenten of predikaten, maar over "states of affairs", "mogelijke werelden", "momenten" of "data" in de tijd, "fasen" in een proces, etc. En daarmee komen we op (o.a.) de modale logica's, zoals ze via de modeltheorie van Kripke e.a. interpreteerbaar zijn geworden (sommige axiomatieken bestonden al een halve eeuw). Dat de modaallogische constanten
"□"
" het is noodzakelijk dat" en
"◊"
"het is mogelijk dat"
niet alleen de interdefinieerbaarheid
"□" = "¬◊¬" en "◊" = "¬□¬"
gemeenschappelijk hebben met de gangbare universele en existentiële kwantoren is gedemonstreerd o.a. door Robert Feys. [3]
Om intuïtief een idee te geven van waar modale logica's eigenlijk over gaan is het het handigst uit te gaan van een interpretatie van de modeltheorie. We zeggen dan dat modale logica's, in tegenstelling tot de gewone, niet slechts een enkele wereld, maar meerdere werelden inventariseren (cf productlogica's). Vaak (Kripke) wordt er dan één afgezonderd als zijnde "de echte"; andere werelden zijn met deze en met elkaar al of niet verbonden door wat Hintikka de "alternativity relation" genoemd heeft: w1Rw2 dan en slechts dan als, gezien vanuit w1, w2 mogelijk is. w2 is dan een "alternatief" voor w1. Deze relatie kan, maar hoeft dat niet, symmetrisch, transitief, reflexief zijn. Met deze keuzevrijheid nu, die in de modellen in te voeren is, corresponderen verschillende in de loop van de laatste vijftig jaar ontwikkelde axiomatieken. Misschien dat dit alles het best duidelijk gemaakt kan worden aan de hand van een enkel op ons onderwerp toegespitst voorbeeld, dat meteen laat zien welke gevarieerde toepassingsgebieden deze soort logica's hebben.
Tijdlogica's worden in de regel opgezet juist vanuit een interpretatie, die aanleiding geeft tot een model dat dan op zijn beurt weer geaxiomatiseerd wordt. In het algemeen zal men zich dan de mogelijke werelden voorstellen als gerangschikt op een rij, die de "tijdlijn" vormt. De alternativiteitsrelatie zal van het nu-moment naar de toekomst-momenten, en van ieder van deze naar de t.o.v. hem weer latere gaan (transitiviteit). Binnen de tijdlogica nu zijn door de grote vernieuwer op dat terrein, A.N. Prior, twee definities van resp. "noodzakelijk" en "mogelijk" aan de orde gesteld, afkomstig van de Griekse wijsgeer Diodorus:
"□p" = "p ∧ Gp"
noodzakelijkerwijze p = p is er nu en zal er altijd zijn
"◊p" = "p ∨ Fp"
mogelijkerwijze p = p is er nu of zal er in de toekomst ooit zijn.
Deze definities hebben veel inkt doen vloeien. De tweede, die de intuïtie misschien het meest tegen de haren instrijkt, wordt veel aannemelijker als men zich de toekomst in de vorm van zich vertakkende tijdlijnen voorstelt; de vertaling luidt dan: mogelijkerwijze p = p is er nu of ligt ergens in een van de toekomstlijnen die vanaf het heden bereikbaar zijn. Modaliteiten die aan deze definities beantwoorden worden Diodorische modaliteiten genoemd. De reden waarom ze hier genoemd zijn is gelegen in het feit dat een specifieke variant ervan uitermate geschikt lijkt om te beschrijven wat we bedoelen als we over "muzikale wetten", of over "wat zou kunnen gebeuren" in een muziek spreken. Maar daarvoor willen we wel uitgaan van een tijdsperspectief dat het omgekeerde is van het zoiuist beschrevene. Dat geeft aanleiding tot Diodorische* modaliteiten. Die laten zich dan als volgt definiëren:
"□p" = "p ∧ Hp"
p is een wet = p is er nu en is er altijd geweest
"◊p" = "p ∨ Pp"
p kan = p is er nu of is er ooit geweest.
Opnieuw is het waarschijnlijk de tweede definitie die de meeste objecties oproept. Hoe haalt een mens het in zijn hoofd de mogelijkheden van een muziek te beperken tot wat ze vóór een bepaald moment gedaan heeft? We geven hier een tweeledig antwoord op. Ten eerste zullen we in de "wetten" die voor kunstproducten gelden een speciaal soort "zwakte" willen inbouwen, die ze onderscheiden kan van b.v. natuurwetten. Ten tweede geldt een zeer essentiële overweging, die mede verband houdt met het gestelde over muziek als 'persoonlijke' zaak.
Ieder stuk muziek, zodra het zich begint af te spelen, of zodra er ook maar iets over bekend is, roept bij de luisteraar associaties, positieve en negatieve, op met muzieken die hij al kent en waar de gegeven muziek mee te maken heeft. Zo kan men stellen dat iedere muziek, zodra hij van start is, zichzelf een "verleden van vóór de eerste maatstreep" verschaft, en dat doet door de relaties die hij heeft met het milieu-van-muzieken waar hij in terecht komt. Ruwweg twee elementen bepalen hoe dat gebeurt. Ten eerste de "objectieve" verbanden en verwantschappen met andere muzieken, en ten tweede een element van subjectiviteit: het antwoord op de vraag welke van die andere muzieken een gegeven luisteraar kent, en hoe hij ze kent. Onze definities worden aanzienlijk plausibeler in dit nieuwe perspectief. Wanneer ik een stuk Bach-achtig van start hoor gaan, houd ik erin voor mogelijk wat, naar mijn mening, in de gegeven soort Bach-muzieken voorkomt. Als ik afwijkingen ga horen wordt mijn zekerheid over wat mogelijk of onmogelijk is minder groot: ik "plaats" het stuk dan anders, en mijn schatting over de muzikale wetten/mogelijkheden ervan past zich aan.
De soort logische modellen die, volgens het voorgaande, vooralsnog het meest geschikt lijken voor onze formalisatieoogmerken zijn gekenmerkt door twee eigenschappen van de relatie R die de mogelijke werelden, c.q. momenten, verbindt. De eerste is reflexiviteit:
(∀wi) (wiRwi)
Toegespitst op de door ons bedoelde interpretatie zouden we de volgende "vertaling" kunnen voorstellen: voor ieder moment in een muziekstuk geldt, dat wanneer het er is, het mogelijk blijkt [4], een stelling waartegen weinigen zullen protesteren. De tweede eigenschap van R is transitiviteit:
(∀wi)(∀wj)(∀wk)((wiRwj ∧ wjRwk) → WiRwk)
Opnieuw toegespitst op ons specifiek gebruik van logische taal weer een "vertaling": Als (1) zich in het verleden van een gegeven moment wi een ander moment wj bevindt, en als (2) dit op zijn beurt wordt voorafgegaan door een derde moment wk, dan behoort wk tot het verleden van wi [5]. Ook dit uitgangspunt is weinig problematisch. Het rekent gewoon op het functioneren van het geheugen, zoals het eerste op ons onmiddellijk waarnemingsvermogen rekent. Iets meer uitleg is vereist voor een laatste eigenschap van het aanbevolen model, die er in axiomatische vorm als volgt uit ziet:
⊢ ◊◊p
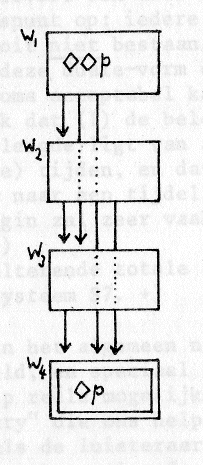
toegespitst vertaalbaar als: In het verleden van ieder muzikaal moment bevindt zich een moment, van waaruit men zich n'importe wat kan herinneren, of: tot de mogelijkheden van iedere muzikale situatie hoort een toestand waarin alles mogelijk is. Deze cryptische uitspraak, die uiteindelijk dienen moet om kunstproducten als muziek te onderscheiden van "de werkelijkheid", kan misschien het best worden verduidelijkt aan de hand van de modeltheorie. Kijken we daarom even naar fig. 1. [6]
 |
(De pijlen geven de R relaties aan (behalve de reflexieve). Let op de transitiviteit; merk op dat de tijd"richting" die voor onze interpretatie relevant is van onderen naar boven is.) |
fig. 1
en overwegen we het volgende. ◊◊p betekent: ooit ◊p. ◊p betekent: n'importe wat is mogelijk. In een wereld of moment waarin ◊p geldt, zijn dus alle uitspraken beginnend met ◊ (of ¬ □) waar, en daarom alle uitspraken beginnend met □ (of ¬ ◊) onwaar. Kripke heeft deze werelden "non-normal worlds" genoemd. Zij bepalen de waarheidswaarden van hun modaliteiten gewoon a priori, en gebruiken dus geen R relaties, zelfs geen reflexieve. Daarom zullen zij in ieder gegeven model, als dat grafisch weergegeven is als in fig. 1, onderaan te vinden zijn.
Eigenlijk geven zij de toestand weer van vóór een muziek begint, als het stuk nog n'importe wat kan zijn, en het is juist het hebben van dit soort "begin", dat kunstproducten onderscheidt van episoden van de werkelijkheid. Een intuïtief plausibel gevolg is verder dat, als equivalent duale van ◊◊p, ¬□□p geldt: niets is noodzakelijkerwijze noodzakelijk: er bestaan geen noodzakelijke wetten in kunstproducten, alleen ad hoc systemen en hun wetten. Ook de interpretatie van ¬□□p met □ als Diodorische* modaliteit levert een voor kunstproducten zeer plausibel uitgangspunt op: iedere "wet" van een gegeven muziek heeft ooit niet bestaan. Misschien is het zodoende vooral deze duale-vorm die onze aanname van ◊◊p als axioma acceptabel kan maken. Gepostuleerd wordt namelijk dat (1) de belevingstijd van een stuk in het verlengde ligt van andere (muzikale en buitenmuzikale) tijden, en dat (2) het begin ervan een overgang is naar een tijdelijk rijk van specifieke wetten. (Dat begin zal zeer vaak voor de eerste maatstreep liggen!) De resulterende totale axiomatiek wordt die van het Lewis-systeem S7. [7]
Omdat in het algemeen niets instruktiever is dan een voorbeeld, en speciaal ook om te laten zien dat ⊢ ◊◊p reële mogelijkheden toevoegt aan de "logical machinery" die ons helpen moet het proces van begrijpen zoals de luisteraar dat meemaakt te formaliseren, werken we het volgende, zeer kleine, concrete geval uit.

fig. 2
De (voorlopige) formalisatie is dan als volgt:
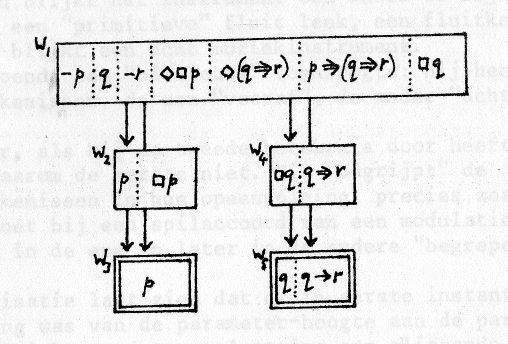
fig. 3
Logische constanten:
¬ = negatie: "niet ..."
→ = materiële implicatie: "als...dan..."
⇒ = strikte implicatie: "α⇒β" is gelijk "□(α→β)"
□ = noodzakelijkerwijze
◊ = mogelijkerwijze
∧ = conjunctie: "...en..."
∨ = disjunctie: "...of..."
Variabelen:
p = q∧r∧ ...
q = omhoogstrevend
r = glissando forte
Het muziekje is erop gemaakt met zo weinig mogelijk noten een zo duidelijk mogelijk muzikaal "effect" te realiseren, waarvan de term "bivalentiefunctie" misschien de beste algemene aanduiding is. Het gaat om het volgende. Het eerste wat men hoort, het g3-c4 glissando, gepaard met crescendo en uitkomend op een vaste, niet vibrerende fortissimo c4, suggereert een sirene- of fluitketelachtige klankbron, waarvoor hoogte aan sterkte gebonden is en waarvan de toptoon c4 is. Dit is een konditionering van de hoorder; er wordt ingespeeld op klankfenomenen die hij kent. Het zo begrepen geluid wordt "p" genoemd. Veel hoorders zullen het niet in parameters analyseren maar het alleen een "soort klankbronnen" associëren. (Zij leggen de weg w3 - w2 - w1 af). Ze moeten hun interpretatie drastisch herzien als de as4, een veel hogere noot, plotseling moeiteloos (ppp) en zonder glissando bereikt wordt. Het hele veld van muzikale mogelijkheden is veranderd. Wat eerst een met moeite (gliss + molto cresc) bereikte top was (c4) blijkt dit achteraf in het geheel niet te zijn. In zekere zin blijkt het instrument een ander te zijn. Wat eerst een "primitieve" fluit leek, een fluitketelfluit, blijkt een echt muziekinstrument. c4 is zodoende een "bivalente" toonhoogte: hij heeft twee betekenissen, de een "vooraf", de ander "achteraf".
De hoorder, als hij de tweede betekenis door heeft, vergeet daarom de eerste niet. Hij "begrijpt" de twee betekenissen in hun opeenvolging, precies zoals hij dat doet bij een spilaccoord van een modulatie, dat eerst in de ene en later in de andere "begrepen" wordt. De formalisatie laat zien dat er in eerste instantie een binding was van de parameter-hoogte aan de parameter-dynamiek, en dat verplaatsing aan glissando was gekoppeld, zozeer dat ze via het hanteren van het fluitketel-beeld zelfs niet meer van elkaar gescheiden gedacht hoefden te worden. De komst van de as4 ppp en sprongsgewijze bereikt dwingt dan plotseling het denken van de hoorder tot het onderscheiden van meer parameters dan eerst.[8] De weg w5 - w4 - w1 wordt afgelegd door een hoorder die analytischer luistert, het begin van het muziekje meteen interpreteert als een binding van parameters aan elkaar, en het juist daarop klasseert. Dat is voor hem dus in eerste instantie de "wet" van het stukje; later blijken de parameters dan toch zelfstandig te kunnen opereren, en blijft alleen de "wet" □q: altijd klimmen, overeind.
Tenslotte ons beloofde voorbeeld van het nut van ⊢ ◊◊p (het nut dus van S7 boven S8 enerzijds en S4 anderzijds). S7 stelt ons in staat "stukken werkelijkheid" in ons formalisatieproces op te nemen en te integreren. Voor sommige 20e-eeuwse activiteiten (surrealisme, happenings, etc.) is dat essentieel. In ons voorbeeld zouden we dan het (aardige) geval kunnen opnemen van de luisteraar die even denkt dat het een echte fluitketel is die hij hoort, en die door het vervolg uit de droom wordt geholpen.
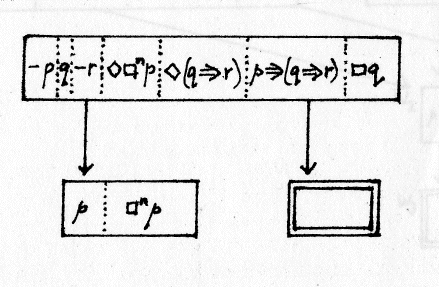 |
Referentie als in fig. 3. □n = n maal geïtereerd □ |
fig. 4
Het totale schema, waarin alle tot nu toe beschouwde denk/ervaringsroutes door ons proefmuziekje zijn vertegenwoordigd volgt dan hierna. We geven de R relatie nog maar met enkele pijlen weer en expliciteren de (overal aanwezige!) transitiviteit niet meer, om het beeld grafisch helder te houden. (N.B. De reflexiviteit is altijd al impliciet gebleven!) De twee mogelijke eindpunten zijn zodoende praktisch gelijk. Alleen wordt van de mensen die nooit gedacht hebben met een echte fluitketel te doen te hebben niet beslist geëist dat ze de mogelijkheid ervan ontdekken. Ze volgen de routes w3 - w2 - w1 òf w5 - w4 - w1 òf w3 - w2 - w6 òf w5 - w4 - w6. Wel wordt het omgekeerde aangenomen: de hoorder die een fluitketel dacht te horen realiseert zich dat anderen zich niet zo hoeven te vergissen. Hij volgt w7 - w6.
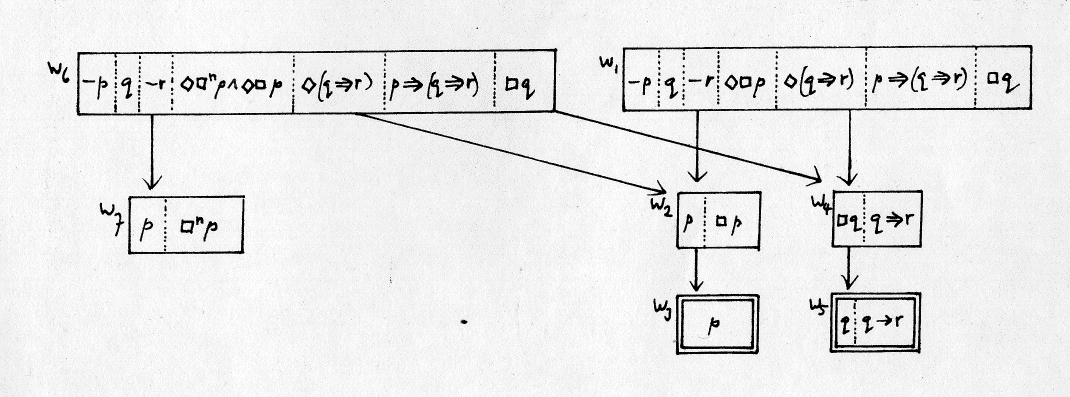
fig. 5
1 In de laatste instantie komt een en ander hierop neer, dat bij wijze van werkdefinitie van "gevoel" de volgende geldt: een gevoel is een "map of the situation", een model van de situatie in mijn bewustzijn, begeleid natuurlijk door alle psychophysiologische bijverschijnselen die erdoor worden veroorzaakt.
2 Natuurlijk zouden wij niet willen suggereren dat de predikaatlogica op zichzelf niet kerngezond zou zijn. De problemen betreffen de toepassing ervan binnen een gegeven referentiekader.
3 "A heuristical approach to modal propositional logic" in Modal Logics, Leuven-Parijs 1965.
4 Axiomatisch: ⊢ p → ◊ p
5 Axiomatisch hier niet in de gangbaarste (S4) vorm ⊢ □ p → □□p, maar om redenen die dadelijk aan de orde komen, in een iets gecompliceerder (S3) versie: ⊢ (p ⇒ q) ⇒ (□p ⇒ □q)
6 Een transitief schema kan natuurlijk o.a. "boom"vormig zijn en mag dat hier ook wat ons betreft. We zullen verder ook niet eisen dat aan het uiteinde van iedere tak zich een "non-normal" wereld bevindt, en dus niet ⊢ □◊◊p (S8) als axioma kiezen.
7 Voor preciezere en verdere informatie zie Hughes & Cresswell, Introduction to Modal Logic, Londen '68.
8 Dergelijke processen, ons aanhalen van modulaties als vergelijkbaar hiermee liet het al zien, zijn zeer fundamentele elementen van het muzikale denken, en kunnen zich op zeer verschillende nivo's manifesteren. Dat onze formalisatie ervan een zekere algemene geldigheid bezit kan blijken uit het feit dat we, door de interpretatie van de variabelen te herschrijven en verder alles intact te laten, formalisaties krijgen van (1) de eerste tien maten van "La sérénade interrompue", nummer 9 uit het eerste boek preludes van Debussy, en van (2) een modulatie.
| (1) | (2) |
| p = q∧r∧ ... q = ambitus producerend r = verticaal zlch bewegend |
p = q∧r∧ ... q = de accoorden opnemend in tonaal-functionele verbanden r = in de toonsoort T staand |
Jos Kunst home page Nederlands | Jos Kunst home page English | Sitemap